Test the accuracy of GPS
Variation in the exact positioning
GPS - Global Positioning System can determine the exact position anywhere on earth. It allows you to navigate to specific geographic coordinates, or saving the current location in memory. With repeated surveys the position of one and the same space apparatus displays a different coordinates. Currently, the position is different from the actual on certain conditions. It is due to the actual GPS technology and other surrounding influences.
Longer time popped into my head at the question of how in practice the true value of this variation, and with what accuracy respectively uncertainty can be recorded or navigate to any location. To find particular values, I do a little experiment that I then evaluated.

Fig.1: Measuring apparatus
I turned the GPS Module LD-3W (hereinafter referred to as GPSK) and start recording the Track. GPSK was still located in the attic of the house. Sky View prevented only tiled roof. GPSK still engages the signals from more than 6 satellites. To determine the latitude and longitude are required a minimum of 3 satellites and for determining your position with altitude 4.
Circulation of the satellite around the Earth takes about 12 hours. Location of GPSK are sending out and storing (via Bluetooth) to a mobile phone in 2 second intervals for more than 12 hours. Thus I gained 20,000 measured data. Before the measurement it is necessary to disable the static navigation, otherwise position will be recorded only when moving GPSK.
One indication of the measured position includes:
- latitude
- longitude
- elevation
- Record date / time

Figure 2: All points scored in 12 hours
Orb.2 on the track log displayed on a calibrated map. Blob looks like a walk in the garden with GPSK but GPSK was still motionless asked at one point. It is a set of coordinates measured with a deviation from the true exact location. Since the actual exact position, I knew I had to fix it somehow. I therefore set point called "center" whose geographic coordinates are determined as the arithmetic average of all measured values for 12 hours. The coordinates of this point I deem the exact location.
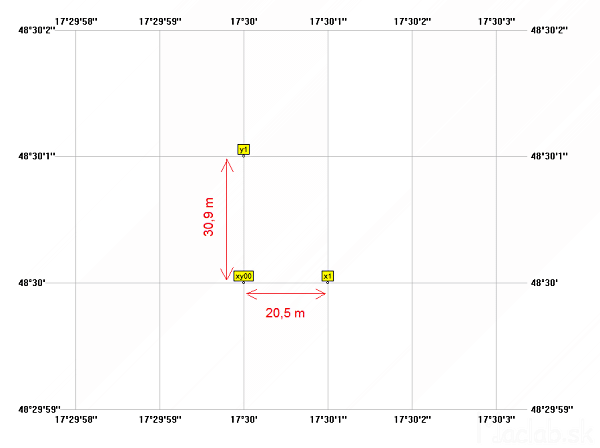
Figure 3: Diagram kovertovania zepepisných coordinates for length units.
Whereas it is mainly interested in how many meters GPSK shows me otherwise, I transferred the geographic coordinates for length units. Very small area on the surface of the Earth can be considered as plane. Elipsodid WGS84 I therefore converted to a rectangular coordinate system. Origin of coordinate system is the same as the position of the "center" and has coordinates [0, 0, 0].
The measured values are converted a follows:
- Latitude -> os y
- Longitude -> OS X
- Altitude -> Z axis
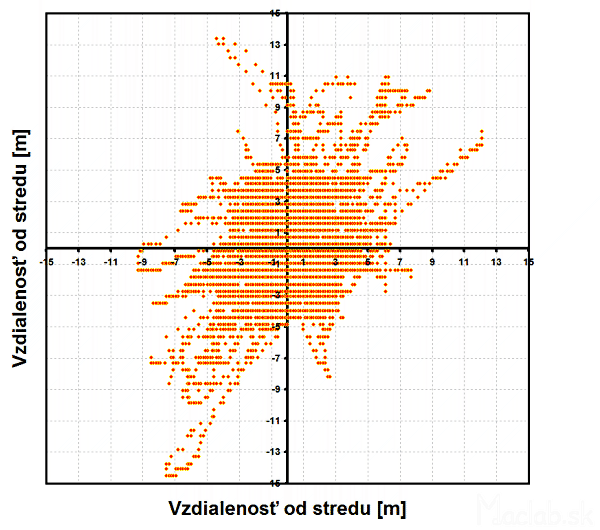
Figure 4: Measured points in the new coordinate system.
Figure 4 displays the measured points in the new coordinate system randomly placed around the center. The calculation of geographic coordinates is mainly dependent on the mutual arrangement of satellites in orbit. The satellites are due to earth moving and thereby changing the calculated position GPSK time.
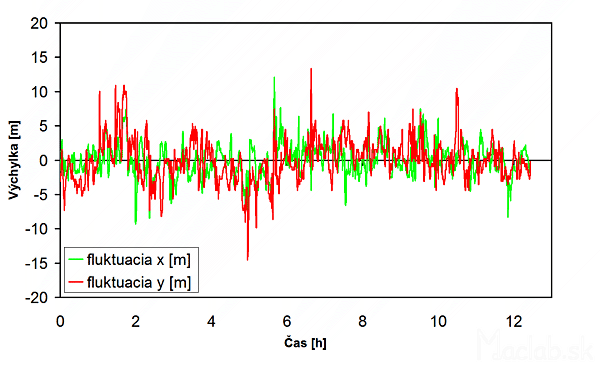
Figure 5: Changing the displacement of the center separately for the x and y.
I depicted in Figure 5, therefore, the deviation of the measured position of the center vs. time, respectively in the direction of the axis x and the axis y. From the picture it is clear that the size of this deflection is changed to almost the same direction of x and y. At the time, it is therefore also loaded identically deviation direction of x and y.
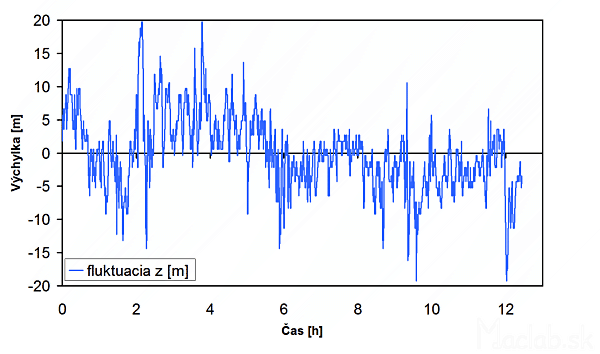
Figure 6: elevation changes over time.
GPS system allows the detection of altitude. It is derived from the spatial coordinates. The measured height is also different changes over time. In our case the displacement of the center in the z direction. Comparing the graphs it can be seen that the values of displacements in the z direction to double the x or the y axis. It's probably due to the fact that the satellites are "watching the GPSK as if from above."
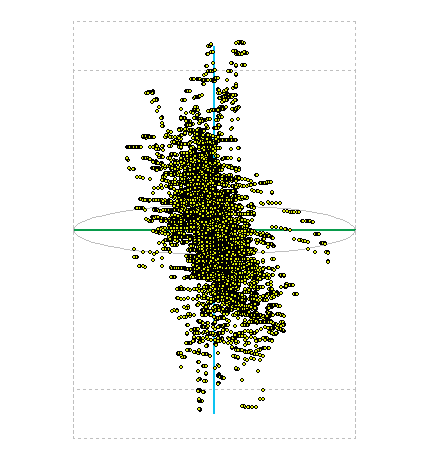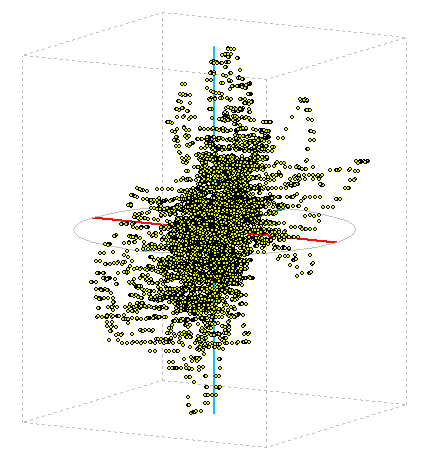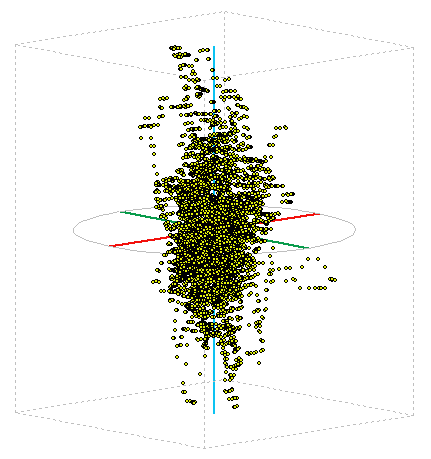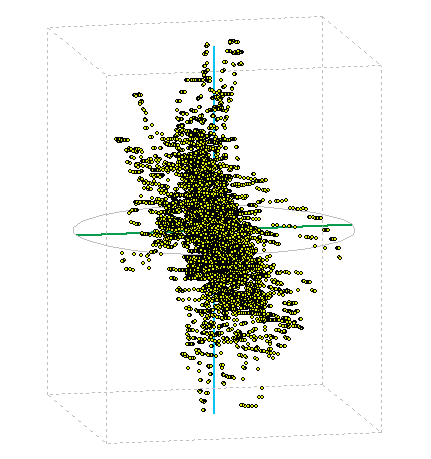
Figure 7: Display of measured position in space.
Deviation from determining the exact position in space is then actually a 3D volume in the shape of a cloud. Figure 7 displays the measured points in 3D space. On the axis of the height in meters, the distance from the middle to the top of the imaginary box is 20m and the distance from center to ORAL block is 15m. The graph as many values of the overlap.
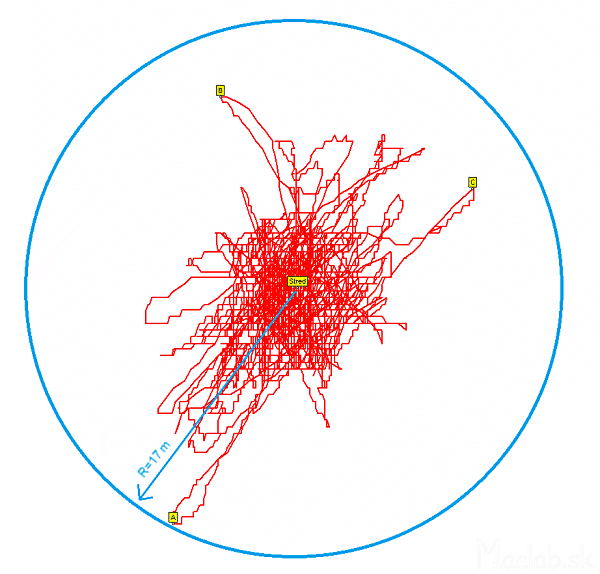
Figure 8: The absolute distance of a point from Wednesday.
The exact determination of the altitude to me it does not matter. It cares about the most exact positioning in the xy plane. I introduced the concept of absolute distance from the center. It is given by the size of the vector, the origin of which is identical to the rectangular coordinate system the beginning and the end point of the vector is the measured point.
Figure 8 Example for the most distant point from the center point was A. The absolute value of the distance from the center point A it is 17 meters.

Figure 9: Change absolute distance with time.
Changes in absolute distance in time I appear in Figure 9. In the picture that turnover absolute distance is often found near the center but less often further away from the center. Right in the middle there was no evidence in either case. It also occurred outside the area or farther apart than 17m.
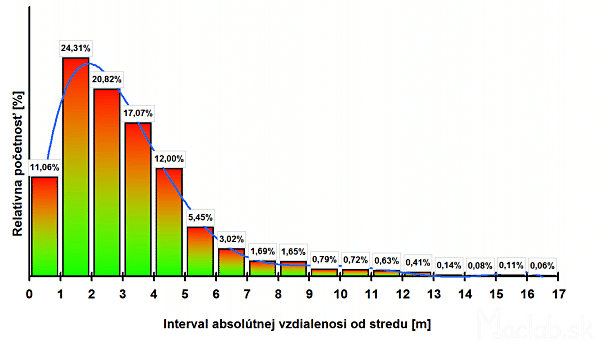
Figure 10: Frequency of set points of the measured values for specific intervals.
17 meters inside the circle I was divided into intervals of one meter spacing. 10 is a frequency value of the absolute distance from the center. The term relative abundance is the number of measured values that fall within the range expressed as a percentage. Is the interval, expressed graphically flat annulus centered at the origin.
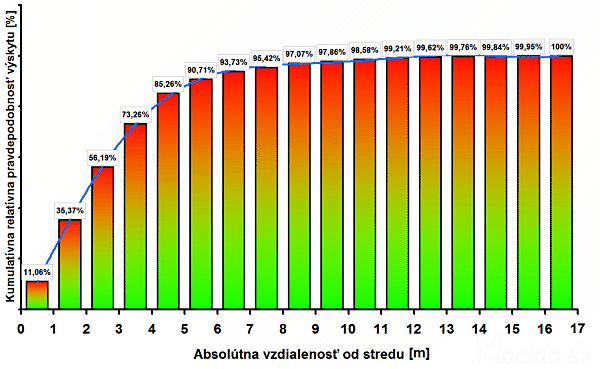
Figure 11: Likelihood of occurrence for a given interval of the absolute distance from the center.
The graph of cumulative relative probability based on previous data relative abundance. It indicates how likely falls into the measured data interval. Graphically the interval, expressed circular area centered at the origin.
The term accuracy, each represents something else. When searching for a lonely tower in the open mind determine position to within 200 meters also. It turns someone bothers to stand on one side of the intersection and a GPS and shows him a position on the opposite side of the intersection.
And here we are finally getting to express accuracy and deviations from the exact location. From Figure 11 it shows that while maintaining those conditions will not be a deviation from the exact location of more than 17m. If I need to determine the position with an accuracy of three meters, I have a 56% probability that the deviation is less than 3 meters. If but merely with an accuracy of 12 meters, I have a 99% probability that we determine the tolerance. Conversely, if I wanted accuracy to 1 mm which is the equivalent of 0.001 meters that trend line (blue curve) quickly drops to 0%.
Me calculated accuracies are valid only if they are respected playing field for determining your position via GPS. At worse conditions could be deviation from the exact position of the more than 100 meters.
Conditions affecting the calculation of the position:
- Obstacles buildings, hills, tree leaves, metal roofs, shading own body, GPSK asked sensor down
- Atmospheric conditions: rain, thick clouds, snow, dust pollution, disturbance of natural origin
- GPS device type GPS chip, an external antenna
- Satellites : The number of captured satellites relative positions change in trajectory, failure, failure, late update
Document provided for derogation would need to make repeated measurements over several days and change the conditions. However, Excel can work simultaneously with only 32000 data. In the future I plan to do even one measurement in the worst conditions. For example, view only a small strip of sky during heavy snowfall.
Related articles: